Applications and Efficiency of Full Wave Rectifier

The maximum efficiency of a full wave rectifier is 81.2%. While minimum efficiency is Zero. The best way to increase the efficiency of rectifier is to use smoothing circuits.

This is the theoretical Interpretation, in this article we are going to learn mathematical Equations of Full wave Rectifier Efficiency.

When I was studying, the question that mostly asked was efficiency, peak factor and form factor with derivation.

And because these equations involves mathematical expressions, this is the part where I and most of the students faced difficulty.

So I decided to include Mathematical derivation of these equations of full wave rectifier also.

Full-wave Rectifier Equations

Every Rectifier type has its own efficiency and other properties. Basically, there are 3 main equations related to full wave rectifier.

1. Efficiency Equation: Tells us how much AC power or AC voltage is used by this rectifier. The result comes in percentage.
2. Form factor
3. Peak factor

I am going to describe all of these one by one in this article.

Full-wave Rectifier Efficiency Equation

The efficiency of a full wave rectifier is defined as the ratio of DC power output to the applied input AC power. Therefore, it is given as;

η = DC Power Output / AC power input

Where η is efficiency.

Full Wave Rectifier Efficiency Calculation:

Let the AC voltage applied (input voltage to be rectified) is v. And as we have to find maximum efficiency, we will take it as variable and suppose it to be V_m sin θ.

Hence

v= V_m sin θ     [ V_m = V_max and as the AC voltage is sinusoidal in nature sin θ will very from 0 to 1]

We take r_f as the forward resistance of crystal diode and R_L be the load resistance of the circuit.

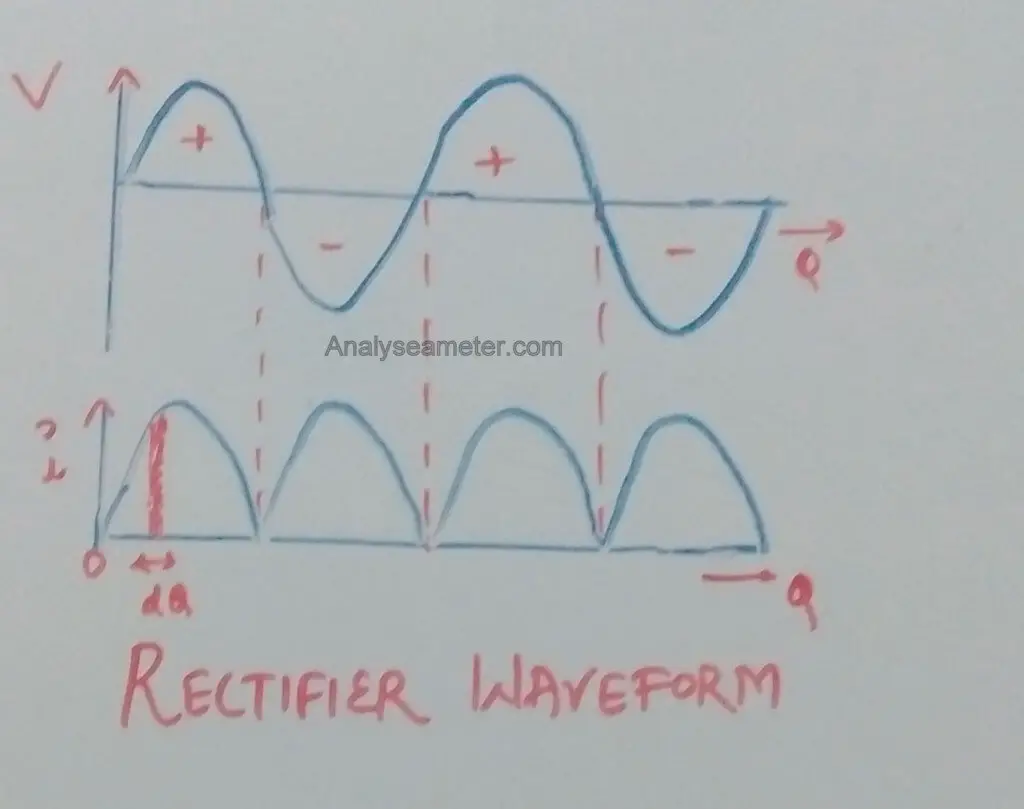
The diagram given below shows the input voltage wave and rectified output wave.

The instantaneous value of current is given by the equation:

i = v / (r_f + R_L)

As we know,

v = V_m sin θ

Therefore,

i = V_m sin θ / (r_f + R_L)

When sin θ = 1, then current = maximum. Therefore,

I_m = V_m / (r_f + R_L)

Where,

 i = I_m sin θ

Since output is obtained across R_L , therefore

D.C power output = I_dc² R_L

                                 = I_av² R_L

Where,

I_av = ʃ (i dθ) / π   ….. (i)

Integrate equation (i) from 0 to π,

 I_av = (1 / π) * ʃ I_m sin θ dθ

     = (I_m / π) * ʃ sin θ dθ

     = (I_m / π) [ – cos θ ]

     = (I_m / π) [ -(-1-1)]

= 2 (I_m / π)

     = (2I_m / π)

Therefore, DC power output is given as,

P_dc = I_dc² R_L = (2I_m / π)² R_L

And AC power input is given as,

P_ac =I_rms² (r_f + R_L)

Where,

** I_rms = √  ʃ (i² dθ) / π ….. (ii)

                     = √ (1 / π) * ʃ I_m² sin² θ dθ

                                  = √ (I_m² / π) * ʃ ( 1- cos 2θ)/ 2  dθ

                                     = √ (I_m² / 2π) * [ ʃ dθ – ʃ cos 2θ dθ ]

                                   = √ (I_m² / 2π) * [[θ] – [sin 2θ / 2]]

                = √ (I_m² / 2π) * [π – 0]

= I_m / √ 2

Therefore, AC power input is given as,

P_ac =I_rms² (r_f + R_L)

      =( I_m / √2)² (r_f + R_L)

As we know,

Rectifier Efficiency (η) = P_dc / P_ac

Put the values of P_dc and P_ac from above equations, therefore,

η =[ (2I_m / π)² * R_L ] / [( I_m / √2)² * (r_f + R_L)]

   = 0.812 R_L / (r_f + R_L)

  = 0.812 / (1+ r_f /R_L)

If r_f is neglected as compared to R_L then the efficiency of the rectifier is maximum. Therefore,

η _max =0.812 = 81.2%

Calculation of Form Factor and Peak factor:

Form factor of Full wave Rectifier:

It is defined as the ratio of RMS value of the output voltage to the average value of the output voltage. Its equation can be given as:

Form Factor = RMS value of the output voltage / average value of the output voltage

= (V_m / √2) / (2 V_m / π) = π / 2 √2

Form Factor = 1.11

Peak Factor of Full wave Rectifier:

It is defined as the ratio of the peak value of the output voltage to the RMS value of the output voltage. Its equation can be given as:

Peak factor = Peak value of the output voltage / RMS value of the output voltage

= V_m / (V_m / √2)

Peak Factor = √2

Applications of Full wave Rectifier:

Full wave rectifier is of two types, center tap and bridge rectifier. Both these rectifiers are used for following purposes depending upon the requirement.

• It can be used to detect the amplitude of modulated radio signal.
• It can be used to supply a polarised voltage in welding.
• It is mainly used in power supply circuits.
• Audio Amplifiers
• Radios
• Home Inverters

Frequently asked Questions about Full wave Rectifier

Q: What is the formula of Full wave rectifier efficiency?

Ans: The formula of efficiency of full wave rectifier is η = DC Power Output / AC power input. Where η is efficiency.

Q: What is the Maximum and minimum efficiency of a Full wave rectifier?

Ans: The maximum efficiency of a full wave rectifier is 81.2%. While minimum efficiency is Zero. Maximum efficiency is obtained when Sin θ is 1 and  Minimum efficiency is when Sin θ is 0.

Q: How do you increase the efficiency of a rectifier?

Ans: The best way to increase the efficiency of rectifier is to use smoothing circuits. Smoothing circuits have smaller ripple value and they also reduce the AC part of the output signal.

Q: What is the form factor of Full wave rectifier?

Ans: The form factor of the full wave rectifier is 1.1. It is the ratio of RMS value of the output voltage to the average value of the output voltage.

Q: What is the Peak factor of Full wave rectifier?

Ans: Peak Factor is the ratio of the peak value of the output voltage to the RMS value of the output voltage. For full wave rectifier it is √2.

Hope you all like this article. For any suggestions please comment below. We always appreciate your suggestions.